How to Save Money with Big Data: Counting Things (Part 2)

I'm often asked about the true scale of systems like YouTube—how many unique users view a video, or how frequently a specific query appears. The numbers quickly shoot into the millions, billions, and beyond (can’t say actual numbers, but it is a lot!). Keeping an exact record for every unique item in these massive data streams would quickly exhaust our memory resources, a problem that deterministic data structures face head-on. This is where Cardinality and Counting Probabilistic Data Structures become our most vital allies.

Estimating Cardinality: Counting the Uniques

Cardinality simply refers to the number of unique elements in a set or stream of data. If you're running an e-commerce platform, your cardinality question is, "How many unique customers bought an item?" If you're running a social media site, it's "How many unique users saw this post?"

Traditional methods, like keeping a massive hash table of every unique ID, become unfeasible. Probabilistic methods overcome this with ingenious algorithms, sacrificing a sliver of accuracy for tremendous space savings.

Linear Counting

The simplest conceptual approach is Linear Counting. Here, we use a large bit array instead of storing the original values. When an element comes in, we hash it and set the corresponding bit in the array to '1'.

The key insight: Collisions (where two different elements hash to the same bit) will occur. However, the number of zeros left in the bit array (V) gives us a way to mathematically estimate the total number of unique items (Estimate) seen, using the formula below, where B is the size of the bit array.

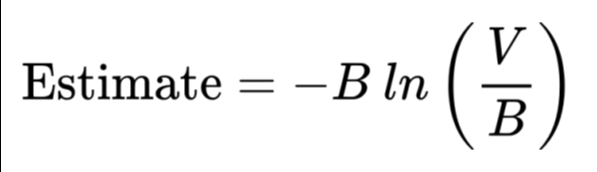
Incredibly simple and would be the first thing I suggest trying.

HyperLogLog (HLL)

For truly massive-scale cardinality estimation, nothing beats HyperLogLog (HLL). HLL uses a statistical technique based on the probability of seeing a long string of leading zeros in the hash value of an element.

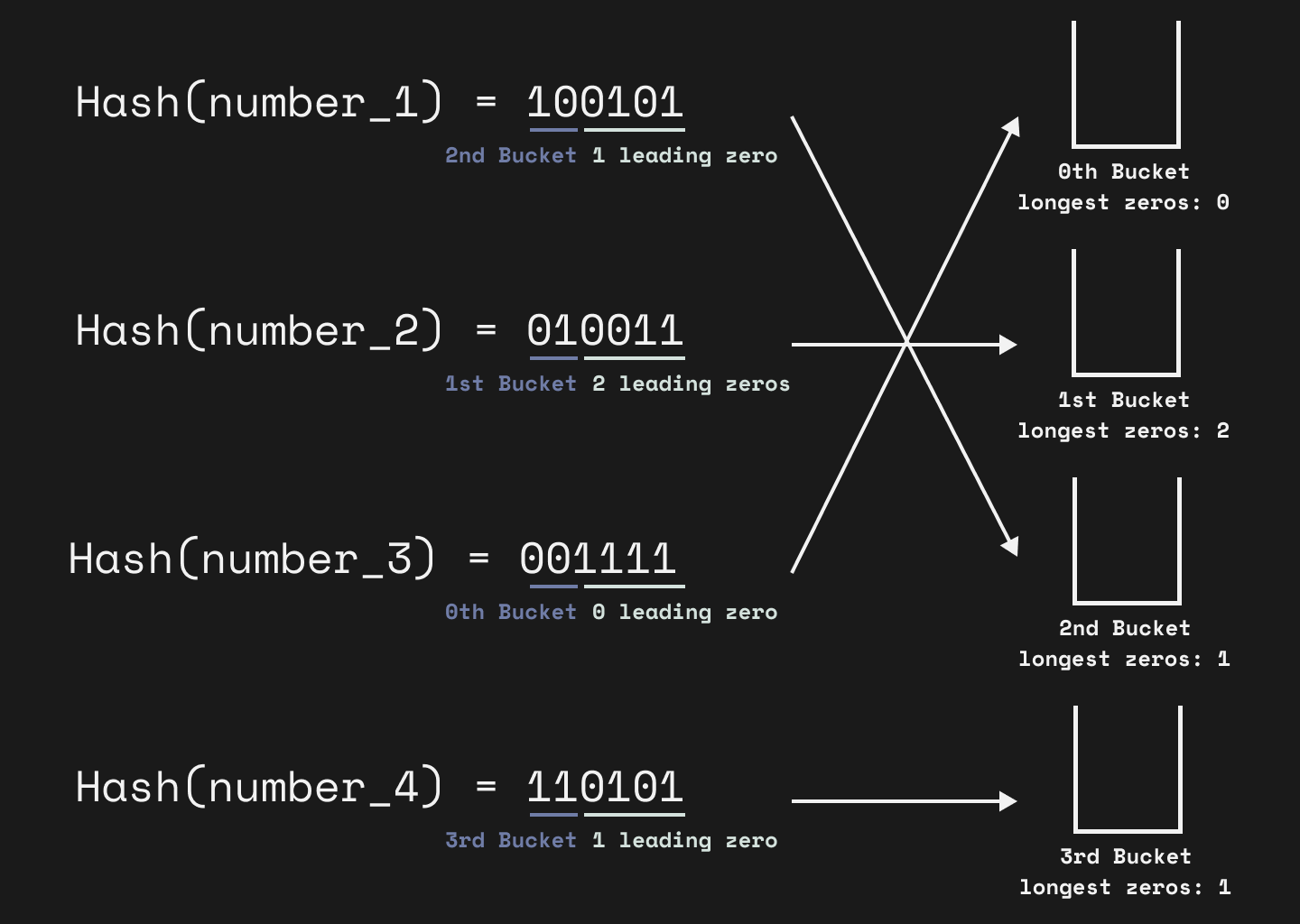
• The lottery analogy: Imagine hashing every unique item to a huge random binary number. The chance of a hash starting with '00000' is much lower than starting with '1', much like the chance of picking the number 1 in a lottery of 100,000 numbers is low. If you've seen a hash with 5 leading zeros, you can statistically infer that you must have already seen a large number of unique items.
• Averaging for Precision: HLL doesn't just rely on one observation; it divides the hash space into buckets (or registers). Each bucket tracks the longest run of leading zeros seen for the items mapped to it. By taking a harmonic mean (a form of weighted average) of the results from all the buckets, the final estimate achieves a high degree of accuracy with an astonishingly low memory footprint. 

Take the previous problem of counting users for a video. I don’t care about tracking user ids, I just want to know the estimated count of unique users. Tracking 10,000,000 users for a video with a list of user ids would take up about 80 MB. 

A standard HLL can estimate a cardinality of over 10,000,000 unique IDs with a ≈4% error using only 2 KB of memory. That's a memory saving of 99.975% compared to storing the actual 8-byte user IDs.

So originally, 10,000,000 videos would have cost us 800 TB or $80,000. With the HLL and all the videos, we only need to store 80 MB, which ranges from $10 to $50. Link

Estimating Frequency: Tracking the "Heavy Hitters"

While cardinality asks "how many unique items," counting (or frequency estimation) asks, "how many times has this item appeared?".

Count-Min Sketch

The Count-Min Sketch (CMS) is the go-to structure for estimating the frequency of elements in a data stream.

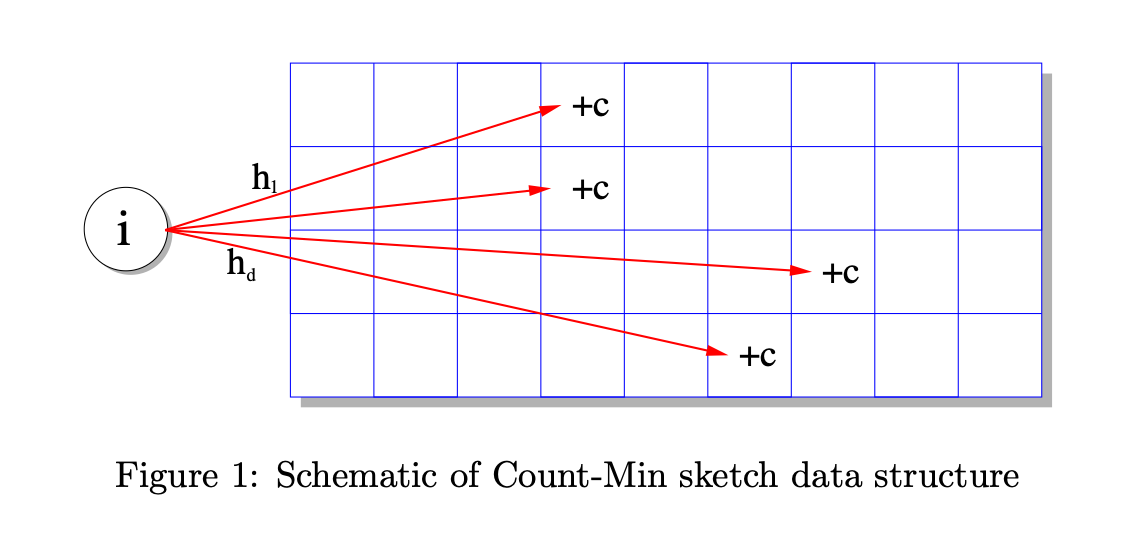
• A Matrix of Counters: It operates using a small, two-dimensional array (a matrix) of counters. Each row in the matrix corresponds to a different hash function.
• The Counting Process: When a new element arrives, we use each of the different hash functions to map the element to a column in its respective row, and then increment the counter at that location.
• The Query Process: To estimate the count for an element, we hash it again using all the hash functions, look up the counter value in each row, and then take the minimum of these values.
• Why the Minimum? Due to collisions, a counter can be incremented by more than one unique element, meaning the count for any single hash function is an overestimation. The true count is likely the smallest one we see, as it represents the least-collided estimate.

Both HyperLogLog and Count-Min Sketch are essential tools for real-time analytics. They allow platforms to process high-velocity data streams and provide key metrics instantly, such as unique users or trending topics, without collapsing under the weight of storing everything.

If you had to choose a single data stream to monitor in real-time—like network packets, trending products, or website clicks—which would it be, and would you prioritize cardinality (uniques) with HLL or frequency (counts) with CMS?