How to Save Money with Big Data: Understanding Hashes (Part 1)

I am currently working with my tutoring student about some computer science data structures and we got to one of my favorite topics, hash functions and tables! And I can’t wait to teach them all about the wonderful world of Probabilistic Data Structures (or PDS). But I realized that not a lot of people know about these things, and they are everywhere, so I decided to write about it.
A “Hash Function” is simply defined as turning an arbitrary long piece of data into a fixed length piece of data. A simple hash function could be just turning the letters of a sentence into numbers and adding them together (like this).
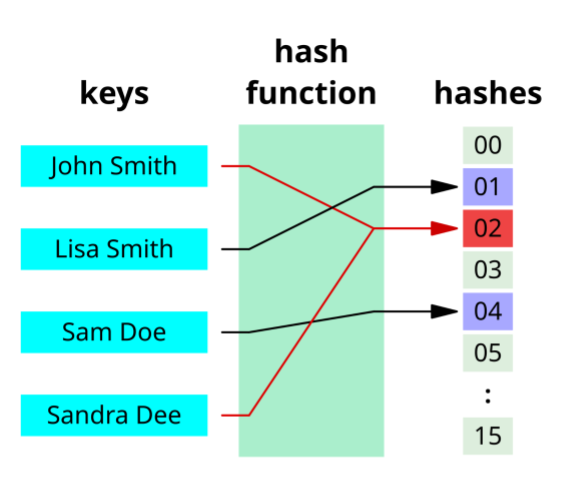
The foundation of nearly all efficient, large-scale data processing rests upon the concept of hashing. Before we can appreciate how probabilistic data structures save us petabytes of memory, we must first clearly understand this building block: the hash function.
What does a Hash Function do?
In its simplest form, a hash function is a mathematical algorithm that takes an input (or a "key") of arbitrary length and produces an output of a fixed, generally much shorter, length. That’s it. Like I mentioned before, a simple hash function could be just turning the letters of a sentence into numbers and adding them together. So if I use the Unicode number for any letter, I can just add up the letters and use that as my hash function.
So imagine a super long sentence.
sentence_1 = """The old lighthouse keeper, Elias, watched the
relentless sweep of the beam cut through the fog, a familiar,
hypnotic rhythm that had governed his life for thirty years.
Outside, the gulls cried a mournful chorus against the steady
roar of the Atlantic, their sound muffled by the thick, salty
air. He remembered a story from his childhood, about a ship
that had mistaken a particularly bright star for its light and
met disaster on the jagged reefs below. Tonight, the sea was a
canvas of inky black, disturbed only by whitecaps that seemed
to grin menacingly in the sparse illumination, a perfect,
lonely night for a man who preferred the company of waves and
silence."""
A hash function can take this and just turn it into a number (what we call a hash number or value).
hash_number_1 = hash_function(sentence_1)
print(hash_number_1)
# prints "85733"
Let’s try it for a different sentence.
sentence_2 = "My name is Zhach, and I like Becky."
hash_number_2 = hash_function(sentence_2)
print(hash_number_2)
# prints "11726"
And the fun part is that those same sentences will always return that same number, no matter what.
hash_number_1 = hash_function(sentence_1)
print(hash_number_1)
# prints "85733"
hash_number_2 = hash_function(sentence_2)
print(hash_number_2)
# prints "11726"
But if you change even one letter (like if you misspell my name), the hash function will return an entirely different number.
sentence_3 = "My name is Zach, and I like Becky."
hash_number_3 = hash_function(sentence_3)
print(hash_number_3)
# prints "69718"
This may seem useless at first, but this can have a number of applications!
- Fixed-Length Conversion: It converts a variable-length key (like a user's full name or a document's title) into a fixed-length value. This is vital for memory efficiency, as a 100-character document title, for example, is consistently represented by a short integer.
- Uniform Distribution: The function is designed to scramble the bits of the input key in such a way that the resulting hash values are distributed as uniformly as possible across the entire keyspace. This minimizes the likelihood of different inputs generating the same output, an event known as a collision (more on that later).
- Table Mapping: Finally, the hash value is typically mapped into an index that is within the size limits of a particular table or array. This is how we achieve the fast lookups associated with data structures like a hash map.
But what if two things get the same number?
Aha! Now you are getting to the tradeoff here. I can take anything and turn it into a number, but the number of possible sentences in the universe have to be greater than the number I can generate in a program right?
This is where collisions come in. Basically, whenever two data points get the same hash value, that is a collision. Like the last sentence I wrote and this other sentence:
sentence_3 = "My name is Zach, and I like Becky."
sentence_4 = "Lz mbme ht Ybch, bnc J kike Cfbkx."
hash_number_3 = hash_function(sentence_3)
hash_number_4 = hash_function(sentence_4)
print(hash_number_3)
# prints "69718"
print(hash_number_4)
# prints "69718"
Two different sentences, but the same number! 🤯
Is this a problem? Depends on the application! How we handle collisions and how often they happen is the knob that most of the upcoming Probabilistic Data Structures really play with.
Accuracy vs. Resources
I believe this is the most important concept to understand when talking about big data systems. The reason hash functions are so important to Probabilistic Data Structures is because they facilitate the biggest trade-off in scalable systems: exchanging perfect accuracy for massive resource savings.
Consider the volume of data that is processed on YouTube, for example. To keep track of every unique user ID for every video impression, for example, would require petabytes of storage. In that scenario, an exact, 100% accurate count is simply infeasible in real-time or too costly to maintain (don’t I know it 😢)
Probabilistic Data Structures, powered by efficient hashing, enable us to answer questions like: "Is this item likely in this set?" or "How many unique items have we seen, with a guaranteed error rate of less than 2%?" In many real-world applications—from web analytics to network traffic monitoring—a highly accurate approximation is not only sufficient but, sometimes, the only viable path to a real-time, scalable solution.
For instance, the user id to video watch problem, I can track all the views on a video with a database of user IDs. If 10 million people watch a video, I am storing 80 MB of data for this 1 video. If I have 10 million videos like this, I am already at 800 TBs of data.
If I use something like a Bloom Filter, I can track all the users for 10 million videos with only 80 TB of memory and a 4% error rate (link). We are saving 90% of the data using a bloom filter!
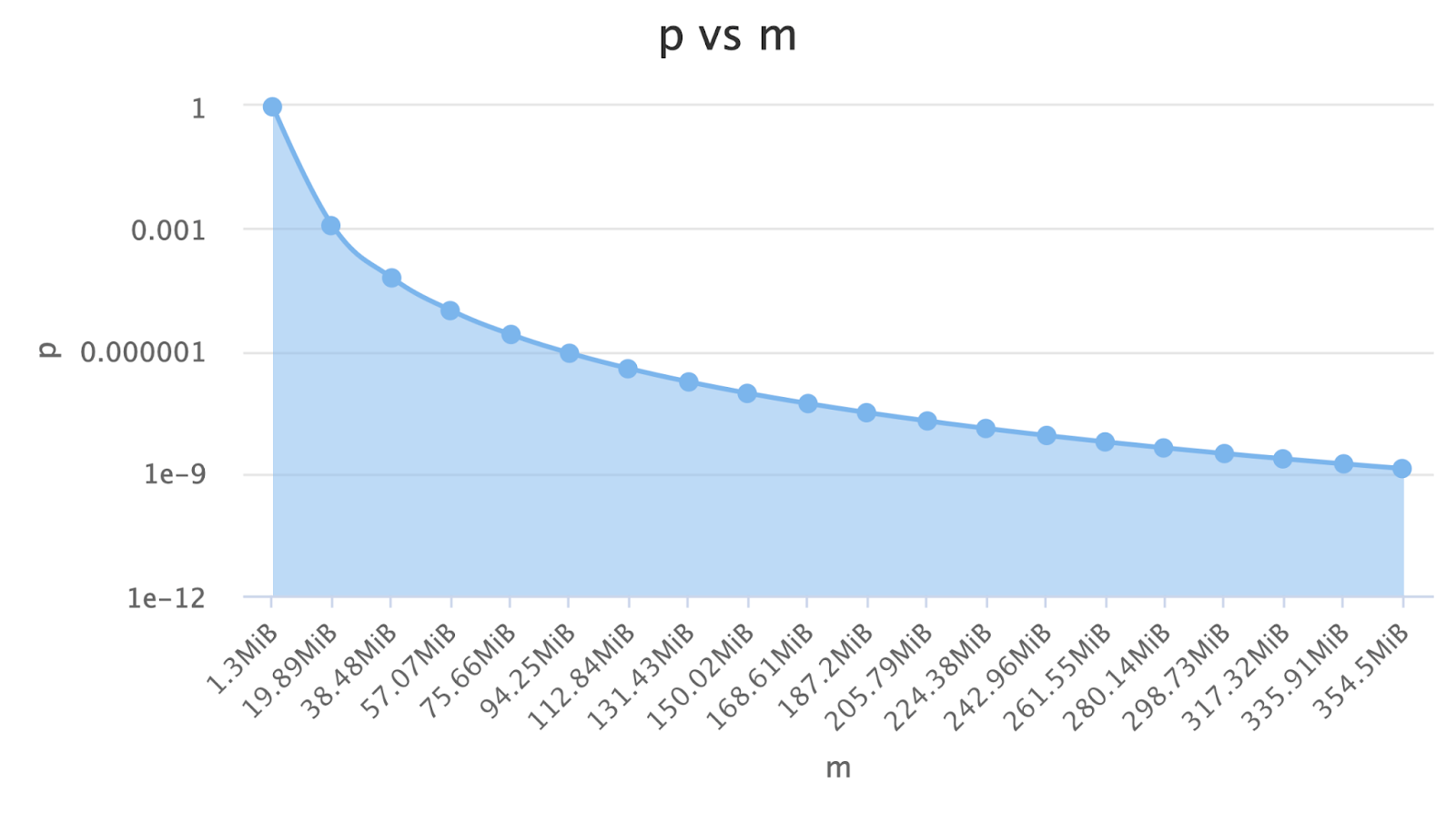
If we say that a Terabyte costs 100$, we saved $72,000 with that change. That’s the power of hashes. We could also increase the memory we use to reduce the error rate, which is a knob that is at our disposal now!
What are some of your favorite examples of where an approximate answer, powered by a simple hash function, is significantly more valuable than a precise one? Share your thoughts below! Follow to read parts 2 and 3!


Comments ()